Phân tích tương quan Pearson là một trong các bước chúng ta thực hiện trong bài nghiên cứu sử dụng phân tích định lượng SPSS. Thường bước này sẽ được thực hiện trước khi phân tích hồi quy.
Mục đích chạy tương quan Pearson nhằm kiểm tra mối tương quan tuyến tính chặt chẽ giữa biến phụ thuộc với các biến độc lập và sớm nhận diện vấn đề đa cộng tuyến khi các biến độc lập cũng có tương quan mạnh với nhau.
1. Lý thuyết về tương quan Pearson
Tương quan tuyến tính giữa hai biến là mối tương quan mà khi biểu diễn giá trị quan sát của hai biến trên mặt phẳng Oxy, các điểm dữ liệu có xu hướng tạo thành một đường thẳng. Theo Gayen (1951) , trong thống kê, các nhà nghiên cứu sử dụng hệ số tương quan Pearson (ký hiệu r) để lượng hóa mức độ chặt chẽ của mối liên hệ tuyến tính giữa hai biến định lượng. Nếu một trong hai hoặc cả hai biến không phải là biến định lượng (biến định tính, biến nhị phân,…) chúng ta sẽ không thực hiện phân tích tương quan Pearson cho các biến này.
Hệ số tương quan Pearson r có giá trị dao động từ -1 đến 1:
- Nếu r càng tiến về 1, -1: tương quan tuyến tính càng mạnh, càng chặt chẽ. Tiến về 1 là tương quan dương, tiến về -1 là tương quan âm.
- Nếu r càng tiến về 0: tương quan tuyến tính càng yếu.
- Nếu r = 1: tương quan tuyến tính tuyệt đối, khi biểu diễn trên đồ thị phân tán Scatter như hình vẽ ở trên, các điểm biểu diễn sẽ nhập lại thành 1 đường thẳng.
- Nếu r = 0: không có mối tương quan tuyến tính. Lúc này sẽ có 2 tình huống xảy ra. Một, không có một mối liên hệ nào giữa 2 biến. Hai, giữa chúng có mối liên hệ phi tuyến.
Andy Field (2009) cho rằng mặc dù có thể đánh giá mối liên hệ tuyến tính giữa hai biến qua hệ số tương quan Pearson, nhưng chúng ta cần thực hiện kiểm định giả thuyết hệ số tương quan này có ý nghĩa thống kê hay không. Kết quả kiểm định nếu sig kiểm định nhỏ hơn 0.05, cặp biến có tương quan tuyến tính với nhau; nếu sig lớn hơn 0.05, cặp biến không có tương quan tuyến tính (giả định lấy mức ý nghĩa 5% = 0.05).
Khi đã xác định hai biến có mối tương quan tuyến tính (sig nhỏ hơn 0.05), chúng ta sẽ xét đến độ mạnh/yếu của mối tương quan này thông qua trị tuyệt đối của r. Theo Andy Field (2009):
- |r| < 0.1: mối tương quan rất yếu
- |r| < 0.3: mối tương quan yếu
- |r| < 0.5: mối tương quan trung bình
- |r| ≥ 0.5: mối tương quan mạnh
2. Phân tích tương quan Pearson trên SPSS 26
Thực hiện phân tích tương quan để đánh giá mối quan hệ giữa các biến bằng cách vào Analyze > Correlate > Bivariate…
Tại đây, chúng ta đưa hết tất cả các biến muốn chạy tương quan Pearson vào mục Variables. Để tiện cho việc đọc kết quả, chúng ta nên đưa biến phụ thuộc lên trên cùng. Trong ví dụ bên dưới biến phụ thuộc là F_HL, các biến còn lại là độc lập. Nhấp vào OK để xác nhận thực hiện lệnh.
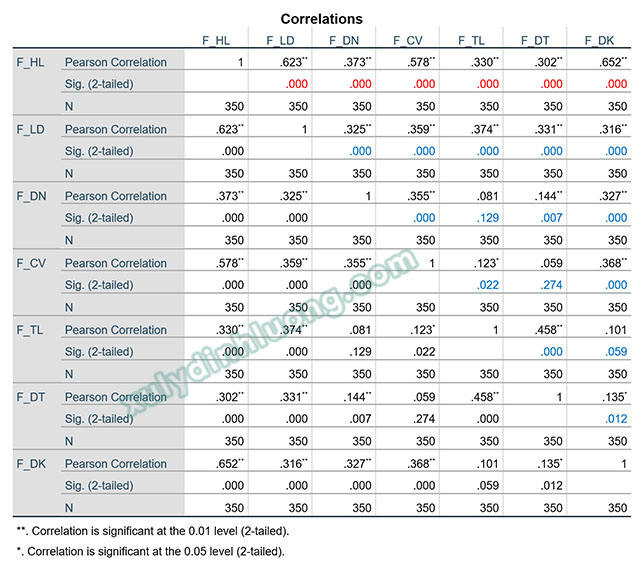
Kết quả tương quan Pearson sẽ được thể hiện trong bảng Correlations. Điểm qua các ký hiệu trong bảng này: Pearson Correlation là hệ số tương quan Pearson (r), Sig. (2-tailed) là giá trị sig của kiểm định t đánh giá hệ số tương quan Pearson có ý nghĩa thống kê hay không, N là cỡ mẫu.
3. Đọc kết quả tương quan Pearson
Chúng ta sẽ xem xét hai loại mối quan hệ tương quan: tương quan giữa biến phụ thuộc với các biến độc lập và tương quan giữa các biến độc lập với nhau. Sở dĩ việc chia ra như vậy, vì sự kỳ vọng về kết quả sẽ có đôi chút khác biệt giữa hai loại mối quan hệ này.
Xem thêm: Giáo trình xử lý SPSS toàn tập có dữ liệu thực hành
3.1 Tương quan giữa biến độc lập với biến phụ thuộc
Trong bảng kết quả bên trên là các giá trị sig được tô màu đỏ. Khi xây dựng mô hình nghiên cứu chúng ta đã tìm hiểu rất kỹ để tìm ra các biến độc lập có sự tác động lên biến phụ thuộc. Việc đưa ra các biến độc lập này dựa trên nền tảng cơ sở lý thuyết, các nghiên cứu tương tự trước đó và sự đánh giá tình hình thực tế tại môi trường khảo sát. Do đó, chúng ta kỳ vọng rằng kết quả phân tích từ dữ liệu sẽ cho thấy các biến độc lập có sự tương quan với biến phụ thuộc hoặc có sự tác động lên biến phụ thuộc. Nếu chúng ta thực hiện phân tích tương quan trước hồi quy, kết quả từ tương quan Pearson cho thấy biến độc lập có tương quan với biến phụ thuộc, khả năng biến độc lập đó sẽ tác động lên biến phụ thuộc ở hồi quy sẽ cao hơn.
Trong bảng kết quả ví dụ, sig kiểm định t tương quan Pearson các giữa sáu biến độc lập F_LD, F_DN, F_CV, F_TL, F_DT, F_DK với biến phụ thuộc F_HL đều nhỏ hơn 0.05. Như vậy, có mối liên hệ tuyến tính giữa các biến độc lập này với biến phụ thuộc.
Kỳ vọng: sig tương quan giữa độc lập với phụ thuộc nhỏ hơn 0.05 và hệ số tương quan càng cao càng tốt.
3.2 Tương quan giữa các biến độc lập với nhau
Trong bảng kết quả bên trên là các giá trị sig được tô màu xanh dương. Tên gọi “biến độc lập” phần nào nói lên được đặc điểm kỳ vọng của dạng biến này: chúng độc lập về ý nghĩa với nhau. Giữa hai biến độc lập nếu có sự tương quan quá mạnh, có khả năng hai biến này bản chất chỉ là một biến, một khái niệm. Hai biến độc lập không có tương quan (sig lớn hơn 0.05) thì gần như không có khả năng xảy ra cộng tuyến giữa hai biến này. Hai biến độc lập có tương quan (sig nhỏ hơn 0.05) và trị tuyệt đối hệ số tương quan lớn hơn 0.7 thì khả năng xảy ra cộng tuyến giữa chúng là tương đối cao (Carsten F. Dormann và các cộng sự, 2013).
Cần lưu ý, khi đánh giá đa cộng tuyến chúng ta nên kết hợp hệ số tương quan Pearson ở bước này cùng với chỉ số VIF trong phân tích hồi quy tuyến tính để có thể đưa ra đánh giá một cách chính xác nhất. Bạn xem cách đánh giá VIF tại bài viết Đa cộng tuyến: Nguyên nhân, dấu hiệu nhận biết và cách khắc phục.
Kỳ vọng: Hệ số tương quan giữa các biến độc lập dưới 0.7.
** Ý NGHĨA 2 DÒNG CUỐI TRONG KẾT QUẢ PEARSON
Khi sig nhỏ hơn 0.05 thì chỗ hệ số tương quan Pearson chúng ta sẽ thấy ký hiệu * hoặc **.
- Ký hiệu ** cho biết rằng cặp biến này có sự tương quan tuyến tính ở mức tin cậy đến 99% (tương ứng mức ý nghĩa 1% = 0.01).
- Ký hiệu * cho biết rằng cặp biến này có sự tương quan tuyến tính ở mức tin cậy đến 95% (tương ứng mức ý nghĩa 5% = 0.05).
Nếu bạn gặp khó khăn khi thực hiện phân tích Pearson hoặc kết quả biến bị loại quá nhiều, bạn có thể tham khảo dịch vụ chạy thuê SPSS của Phạm Lộc Blog hoặc liên hệ trực tiếp zalo/hotline 093 395 1549.