Thực hiện phân tích EFA chung hay riêng biến độc lập với biến phụ thuộc là vấn đề có khá nhiều các bạn, các anh/chị thắc mắc khi phân tích định lượng với SPSS. Chúng ta sẽ cùng đi vào phân tích lý do tại sao chạy chung hay chạy riêng trong bài viết này.
1. Quan điểm của một số nhà nghiên cứu
1.1 Quan điểm của Nguyễn Đình Thọ (2012)
Trong phân tích nhân tố EFA, khi sử dụng phép quay vuông góc thì không được đưa biến phụ thuộc vào chung với biến độc lập vào cùng lúc để thực hiện EFA. Bởi khi sử dụng phép quay vuông gốc, các nhân tố phải không có mối tương quan với nhau, nghĩa là không có sự định nghĩa độc lập với phụ thuộc.
→ Do vậy, nếu chúng ta sử dụng phép quay Varimax hay bất kỳ phép quay vuông góc nào thì cần phân tích EFA riêng giữa độc lập và phụ thuộc, không được đưa tất cả 2 nhóm biến này vào phân tích chung 1 lần.
1.2 Quan điểm của Hair và cộng sự (2010)
Trích nguyên bản: "Mixing dependent and independent variables in a single factor analysis and then using the derived factors to support dependence relationships is inappropriate".
Tạm dịch: Việc gộp chạy chung các độc lập và phụ thuộc trong một phân tích nhân tố khám phá và sau đó lại kiểm tra các mối quan hệ phụ thuộc là không phù hợp.
→ Giải thích chi tiết hơn câu nói này. Nghĩa là khi chúng ta thực hiện phân tích EFA, việc cho chung các biến độc lập và phụ thuộc vào chạy cùng là không hợp lý. Bởi với một đề tài đã xác định được độc lập và phụ thuộc, nghĩa là ngay từ đầu chúng ta đã mặc định xuất hiện mối quan hệ phụ thuộc giữa 2 nhóm biến: một nhóm là tác động lên biến khác và một nhóm là chịu tác động của biến khác.
1.3 Quan điểm của Hair và cộng sự (2015)
Trích nguyên bản: "When you use exploratory factor analysis the variables are not divided into dependent and independent categories. Instead, all variables are analyzed together to identify underlying patterns or factors. The technique can be used to factor analyze either independent or dependent variables considered separately".
Tạm dịch: Khi bạn sử dụng phân tích nhân tố khám phá, các biến không được chia thành phụ thuộc và độc lập. Thay vào đó, tất cả các biến được phân tích cùng nhau để xác định cấu trúc các nhân tố. Kỹ thuật thực hiện phân tích nhân tố khám phá cần được xem xét chạy riêng giữa các biến độc lập và biến phụ thuộc.
→ Cũng như quan điểm thứ 2. Các biến được đưa cùng nhau vào phân tích EFA phải là cùng một loại độc lập hoặc cùng 1 loại phụ thuộc. Không được gộp chung cả 2 loại biến này vào phân tích EFA một lần.
Qua các quan điểm đưa ra ở trên, chúng ta có thể kết luận lại:
- Nếu mô hình đã xác định được biến độc lập và biến phụ thuộc, chúng ta sẽ phân tích EFA riêng giữa độc lập và phụ thuộc.
- Nếu mô hình không phân biệt biến độc lập và biến phụ thuộc, chúng ta có thể phân tích EFA chung giữa độc lập và phụ thuộc.
2. Lý giải vì sao nên chạy chung, vì sao nên chạy riêng
Trước hết chúng ta sẽ xem xét lại mối quan hệ giữa hai loại biến độc lập và phụ thuộc. Sở dĩ chúng ta xác định biến X là độc lập, biến Y là phụ thuộc bởi trên các lý thuyết nền hoặc các nghiên cứu trước đó đã chứng minh rằng X sự có tác động lên Y. Khi X có tác động lên Y, giữa X và Y trong hầu hết các trường hợp sẽ có sự tương quan từ mức trung bình đến mạnh. Sự tương quan này làm cho tính phân biệt giữa X và Y không cao.
Trong EFA, dù có dùng phép trích và phép xoay gì đi nữa thì EFA luôn có một chức năng là đánh giá tính phân biệt của các cấu trúc biến. Khi tính phân biệt được thõa mãn, mỗi nhóm biến sẽ được tách thành một cột trong bảng ma trận xoay. Nếu chúng ta đưa biến phụ thuộc và độc lập vào cùng phân tích chung EFA, sự tương quan mạnh giữa độc lập với phụ thuộc khiến cho các biến quan sát của cấu trúc biến phụ thuộc dễ bị nhập chung vào với các biến độc lập. Điều này làm cho các cấu trúc thang đo không đảm bảo được tính phân biệt trong EFA (tình trạng ma trận xoay lộn xộn). Nên việc chạy EFA riêng độc lập và riêng phụ thuộc là cách chạy tối ưu nhất, vừa hợp lý về tính chất tương quan giữa các biến, vừa phù hợp theo quan điểm của các tác giả nổi tiếng ở trên.
Từ các lý luận ở trên, chúng ta có thể phân chia mô hình nghiên cứu thành hai loại tương ứng với hai phương pháp chạy EFA. Chúng ta cần làm rõ trước về vai trò biến trung gian, biến này vừa đóng vai trò độc lập, vừa đóng vai trò phụ thuộc. Do vậy, khi mình đề cập tới số lượng biến phụ thuộc, số lượng biến độc lập, thì biến trung gian được tính cho cả hai loại biến này.
- Mô hình đơn giản: Là dạng mô hình mà vai trò biến được xác định rõ ràng, số lượng biến phụ thuộc ít, số lượng biến độc lập nhiều, có nhiều biến độc lập tác động vào một biến phụ thuộc → Chạy EFA riêng độc lập, riêng trung gian, riêng phụ thuộc.
- Mô hình phức tạp: Là dạng mô hình mà vai trò biến vẫn có thể xác định được vai trò, tuy nhiên biến đóng vai trò trung gian có số lượng nhiều, các mối quan hệ tác động chằng chịt, số lượng biến phụ thuộc nhiều, có nhiều mối quan hệ mà chỉ một biến độc lập tác động lên một biến phụ thuộc → Chạy EFA chung cho tất cả nếu kết quả tốt, nếu kết quả không tốt, chạy riêng theo vai trò biến. Chúng ta lựa chọn chạy chung bởi vì khi chạy riêng thì số lần EFA quá nhiều và số nhóm biến tham gia vào EFA quá ít. Nhưng nếu chạy chung kết quả quá tệ thì chúng ta quay về nguyên tắc chạy EFA riêng theo vai trò biến độc lập - phụ thuộc.
Đánh giá quan điểm: Mô hình chạy CFA, SEM thì phân tích EFA chung tất cả các biến.
→ Đây là nhận định không có cơ sở và nó chỉ phù hợp cho một số trường hợp nhất định. Do vậy, bạn không nên áp dụng nó một cách cứng nhắc cho mọi trường hợp. Việc bạn xử lý mô hình đường dẫn bằng hồi quy hay SEM đi nữa cũng không liên quan đến việc phân tích EFA chung hay riêng giữa các biến.
Phân tích EFA chung/riêng hoàn toàn dựa vào tính chất mô hình đơn giản hay phức tạp, hay nói cách khác nó phụ thuộc vào vai trò các biến trong mô hình. Nếu mô hình có ít biến trung gian, ít phụ thuộc, nhiều biến độc lập thì bạn nên phân tích EFA riêng. Nếu mô hình có ít biến độc lập, nhiều biến trung gian, mối quan hệ các biến phức tạp bạn nên bỏ qua EFA hoặc phân tích EFA chung.
Nguồn gốc dẫn đến nhận định Mô hình chạy CFA, SEM thì phân tích EFA chung tất cả các biến là bởi vì mô hình SEM thường là các dạng mô hình phức tạp, có khá nhiều biến trung gian. Nhưng:
- Không phải mô hình SEM lúc nào cũng ở dạng phức tạp. Có những mô hình SEM khá đơn giản, biến trung gian ít, biến độc lập nhiều, vai trò biến được xác định một cách tương đối dễ dàng. Những trường hợp như vậy chúng ta chạy EFA riêng các nhóm biến là giải pháp tối ưu nhất.
- Không phải CFA, SEM là phải dùng cho mô hình phức tạp. Chúng ta vẫn sử dụng CFA và SEM cho các mô hình đơn giản một cách hoàn toàn bình thường. Hai kiểm định được sinh ra để đánh giá mọi dạng mô hình chứ không phải chỉ dùng cho dạng mô hình phức tạp. Khi mô hình của bạn ở dạng đơn giản, vai trò biến được xác định một cách dễ dàng, bạn nên chạy EFA riêng các nhóm biến, sau đó tiến hành phân tích CFA chung các nhóm biến một cách bình thường.
Để các bạn dễ hình dung hơn, chúng ta sẽ đi qua hai ví dụ rất cơ bản về hai dạng mô hình ở trên.
Nếu bạn gặp khó khăn khi thực hiện phân tích EFA như biến bị loại nhiều, ma trận xoay lộn xộn, không đảm bảo hội tụ và phân biệt, bạn có thể tham khảo dịch vụ chạy SPSS thuê của Phạm Lộc Blog hoặc liên hệ trực tiếp email xulydinhluong@gmail.com.
2.1 Mô hình đơn giản
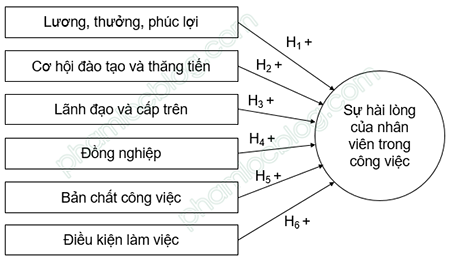
Đây là dạng mô hình phổ biến được sử dụng trong các đề tài nghiên cứu dạng luận văn tốt nghiệp, luận văn thạc sĩ và các nghiên cứu khoa học cấp độ cơ bản. Đặc điểm dạng mô hình này là xác định được các biến độc lập và biến phụ thuộc. Biến phụ thuộc là biến được hướng mũi tên vào (nghĩa là chịu tác động của biến khác), biến độc lập là nơi xuất phát của gốc mũi tên (nghĩa là tác động lên biến khác).
Mũi tên xuất hiện trong mô hình này là mũi tên một chiều hướng từ biến độc lập đến biến phụ thuộc, không có sự xuất hiện mũi tên tác động ngược lại từ phụ thuộc về độc lập. Hoặc nếu có thêm sự xuất hiện của biến trung gian thì chúng ta vẫn dễ dàng xác định được vai trò độc lập, phụ thuộc trong các mối quan hệ tác động. Số lượng biến phụ thuộc trong mô hình ít, số lượng biến độc lập nhiều, có nhiều biến độc lập cùng tác động lên phụ thuộc.
→ Dạng mô hình này khi phân tích nhân tố EFA chúng ta nên phân tích EFA riêng từng nhóm biến.
2.2 Mô hình phức tạp
Đây là dạng mô hình phức tạp hơn. Đặc điểm dạng mô hình này là việc xác định được biến độc lập và biến phụ thuộc khó khăn bởi hướng mũi tên phức tạp và có quá nhiều biến trung gian.
Cắt ra từng mối quan hệ tác động đơn, dễ dàng thấy được một mối tác động đa phần chỉ là một biến độc lập tác động lên một biến phụ thuộc, số lượng biến phụ thuộc nhiều.
→ Dạng mô hình này khi phân tích nhân tố EFA chúng ta nên phân tích EFA chung cho tất cả.
3. Ví dụ chạy riêng các biến trong EFA
Dựa trên quan điểm của Hair và cộng sự, chúng ta sẽ có cách thức chạy riêng cho một số mô hình ví dụ sau đây. Các bạn có thể chạy chung tùy ý, nhưng nếu chạy chung kết quả không tốt bạn hãy chạy riêng theo vai trò độc lập - phụ thuộc. Cơ chế chạy riêng này là hoàn toàn có cơ sở vững chắc dựa trên bản chất tương quan các biến trong mô hình, đồng thời cũng phù hợp với quan điểm của Hair và cộng sự.
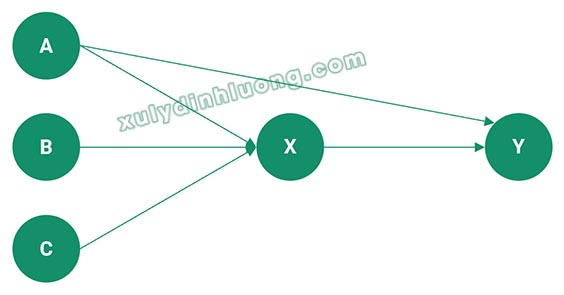
Mô hình 1:
Bước 1: Phân tích quan hệ biến trong mô hình:
- X là biến phụ thuộc của A, B, C. Do đó X sẽ có khả năng tương quan mạnh với A-B-C. Chúng ta phải chạy hai lần EFA: lần một cho 3 biến độc lập A, B, C và lần hai cho cho biến phụ thuộc X.
- Z là biến phụ thuộc của A, B, C. Do đó Z sẽ có khả năng tương quan mạnh với A-B-C. Chúng ta phải chạy hai lần EFA: lần một cho 3 biến độc lập A, B, C và lần hai cho cho biến phụ thuộc Z.
- Do X và Z đều là biến phụ thuộc của A, B, C nên X và Z có khả năng tương quan mạnh với nhau. Chúng phải chạy hai lần EFA: lần một cho X, lần hai cho Z.
- Y là biến phụ thuộc của X, Z. Do đó Y sẽ có khả năng tương quan mạnh với X-Z. Chúng ta phải chạy hai lần EFA: lần một cho 2 biến độc lập X, Z và lần hai cho cho biến phụ thuộc Y.
Bước 2: Xác định số lần EFA
Từ phần phân tích ở bước 1, chúng ta có được 4 lần chạy EFA sau đây:
- EFA cho ba biến độc lập A, B, C.
- EFA cho biến X
- EFA cho biến Z
- EFA cho biến Y
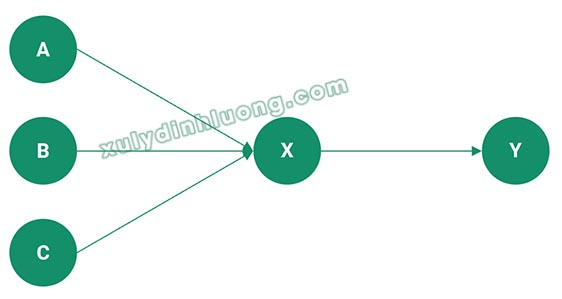
Mô hình 2:
Bước 1: Phân tích quan hệ biến trong mô hình:
- X là biến phụ thuộc của A, B, C. Do đó X sẽ có khả năng tương quan mạnh với A-B-C. Chúng ta phải chạy hai lần EFA: lần một cho 3 biến độc lập A, B, C và lần hai cho cho biến phụ thuộc X.
- Y là biến phụ thuộc của X, A. Do đó Y sẽ có khả năng tương quan mạnh với X-A. Chúng ta phải chạy hai lần EFA: lần một cho 2 biến độc lập X, A và lần hai cho cho biến phụ thuộc Y.
Bước 2: Xác định số lần EFA
Từ phần phân tích ở bước 1, chúng ta có được 3 lần chạy EFA sau đây:
- EFA cho ba biến độc lập A, B, C.
- EFA cho biến X
- EFA cho biến Y
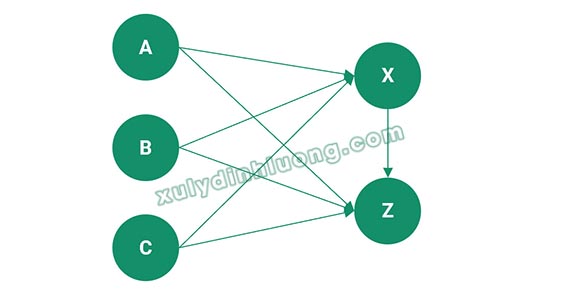
Mô hình 3:
Bước 1: Phân tích quan hệ biến trong mô hình:
- X là biến phụ thuộc của A, B, C. Do đó X sẽ có khả năng tương quan mạnh với A-B-C. Chúng ta phải chạy hai lần EFA: lần một cho 3 biến độc lập A, B, C và lần hai cho cho biến phụ thuộc X.
- Y là biến phụ thuộc của X. Do đó Y sẽ có khả năng tương quan mạnh với X. Chúng ta phải chạy hai lần EFA: lần một cho biến độc lập X và lần hai cho cho biến phụ thuộc Y.
Bước 2: Xác định số lần EFA
Từ phần phân tích ở bước 1, chúng ta có được 3 lần chạy EFA sau đây:
- EFA cho ba biến độc lập A, B, C.
- EFA cho biến X
- EFA cho biến Y
Mô hình 4:
Bước 1: Phân tích quan hệ biến trong mô hình:
- X là biến phụ thuộc của A, B, C. Do đó X sẽ có khả năng tương quan mạnh với A-B-C. Chúng ta phải chạy hai lần EFA: lần một cho 3 biến độc lập A, B, C và lần hai cho cho biến phụ thuộc X.
- Z là biến phụ thuộc của A, B, C. Do đó Z sẽ có khả năng tương quan mạnh với A-B-C. Chúng ta phải chạy hai lần EFA: lần một cho 3 biến độc lập A, B, C và lần hai cho cho biến phụ thuộc Z.
- Z là biến phụ thuộc của X. Do đó Z sẽ có khả năng tương quan mạnh với X. Chúng ta phải chạy hai lần EFA: lần một cho biến độc lập X và lần hai cho cho biến phụ thuộc Z.
Bước 2: Xác định số lần EFA
Từ phần phân tích ở bước 1, chúng ta có được 3 lần chạy EFA sau đây:
- EFA cho ba biến độc lập A, B, C.
- EFA cho biến X
- EFA cho biến Z
Nguồn tham khảo: