Giá trị hội tụ (convergent validity) và giá trị phân biệt (discriminant validity) là hai loại giá trị quan trọng trong đánh giá mối quan hệ giữa các cấu trúc biến. Chúng ta thường gặp hai loại giá trị này trong các kiểm định như EFA (SPSS), CFA (AMOS), Measurement Model (SMARTPLS). Tuy nhiên, nhà nghiên cứu có xu hướng xem xét kỹ hơn hai loại giá trị này trong đánh giá mô hình đo lường của SEM (CFA hoặc Measurement Model) so với EFA trên SPSS.
1. Giá trị hội tụ/tính hội tụ là gì?
Giá trị hội tụ liên quan tới đánh giá mô hình đo lường (CFA trên AMOS và Measurement Model trên SMARTPLS). Việc xây dựng các biến quan sát (chỉ báo) để đảm bảo các biến này đạt được mức độ hội tụ cần thiết sẽ khác nhau ở mô hình đo lường kết quả (reflective) và mô hình đo lường nguyên nhân (formative) (xem sự khác biệt hai dạng mô hình này tại đây).
a. Giá trị hội tụ với mô hình đo lường kết quả
Phần lớn các thang đo trên thực tế được xây dựng theo dạng kết quả nhiều hơn ở dạng nguyên nhân. Đánh giá tính hội tụ cho thang đo kết quả cũng đơn giản hơn rất nhiều so với dạng thang đo nguyên nhân.
Đối với mô hình đo lường kết quả, giá trị hội tụ đề cập tới mức độ tương quan giữa các biến quan sát mà các biến này đo lường cho cùng một khái niệm (Cooper và cộng sự, 2014). Nói một cách dễ hiểu hơn, tính hội tụ chính là việc các biến quan sát của một biến tiềm ẩn có tương quan thuận với nhau không và sự tương quan thuận đó mạnh tới mức độ nào.
Xuất phát từ lý thuyết về mô hình đo lường kết quả, các chỉ báo phản ánh kết quả mạnh từ biến tiềm ẩn nên hệ số tương quan giữa các cặp chỉ báo cần dương và có giá trị cao (Cor(xi, xj) > 0). Từ đó, khi nhà nghiên cứu xây dựng các chỉ báo để phân tích trên thực nghiệm, các chỉ báo này cần thỏa mãn tiêu chí trên. Nếu không, các chỉ báo không đạt được giá trị hội tụ. Nói cách khác, các chỉ báo mà chúng ta xây dựng để đo lường biến tiềm ẩn là chưa phù hợp. Hậu quả, nếu chúng ta sử dụng giá trị của các chỉ báo này để tính toán cho biến tiềm ẩn, giá trị mà biến tiềm ẩn nhận được sẽ không chính xác.
b. Giá trị hội tụ với mô hình đo lường nguyên nhân
Đối với mô hình đo lường nguyên nhân, giá trị hội tụ thể hiện qua mức độ mà các chỉ báo giải thích được sự thay đổi của biến tiềm ẩn. Từ lý thuyết mô hình đo lường nguyên nhân, các chỉ báo là từng thành phần của biến tiềm ẩn, vì thế nếu từng thành phần yếu hoặc không xây dựng đủ các thành phần, mức độ giải thích của các chỉ báo dành cho biến tiềm ẩn sẽ thấp. Hậu quả, sai số đo lường dành cho biến tiềm ẩn sẽ cao hay giá trị biến tiềm ẩn nhận được có độ chính xác không cao.
Do đặc điểm của thang đo nguyên nhân là các biến quan sát không nhất thiết phải có sự tương quan với nhau nên việc đánh giá tính hội tụ dạng thang đo này khá khó khăn. Một số nhà nghiên cứu chọn bỏ qua việc đánh giá, một số khác sử dụng đến biến tổng quát (global variable) và xử lý trên các phần mềm PLS-SEM như SMARTPLS. Bạn có thể xem cách thực hiện kỹ thuật này tại bài viết Đánh giá mô hình đo lường dạng nguyên nhân trên SMARTPLS.
2. Giá trị phân biệt/tính phân biệt là gì?
Giá trị phân biệt liên quan tới mức độ không tương quan giữa một tập chỉ báo dùng để đo lường cho khái niệm này đối với một tập chỉ báo dùng để có lường cho khái niệm khác (Cooper và cộng sự, 2014). Giá trị phân biệt hiện chỉ được áp dụng cho các khái niệm được đo lường dạng thang đo kết quả.
Giá trị phân biệt có liên quan tới mô hình cấu trúc (SEM) và các khái niệm trong mô hình cấu trúc được đo lường bởi các biến tiềm ẩn mà các biến tiềm ẩn lại phải đo lường thông qua các chỉ báo. Nếu một hoặc nhiều chỉ báo cùng đo lường cho hai biến tiềm ẩn trở lên, giá trị của các biến tiềm ẩn này càng có xu hướng dao động giống nhau.
Khi sử dụng bảng câu hỏi để khảo sát, một trong những điều kiện cần để đảm bảo tính phân biệt đó là nội dung của một chỉ báo bất kỳ trong một tập chỉ báo phải khác biệt với nội dung của tất cả các chỉ báo trong một tập chỉ báo khác (đo lường khái niệm khác). Ví dụ, tập chỉ báo thứ nhất có 4 câu hỏi để đo lường cho khái niệm X, tập chỉ báo thứ hai có 3 câu hỏi để đo lường cho khái niệm Y. Khi đó, từng câu hỏi đo lường cho khái niệm X sẽ khác biệt về ý nghĩa so với 3 câu hỏi đo lường cho khái niệm Y. Nói theo một cách khác, đánh giá giá trị phân biệt chính là đánh giá mức độ không tương quan giữa các tập chỉ báo đo lường cho các khái niệm khác nhau.
3. Ví dụ về tính hội tụ, tính phân biệt
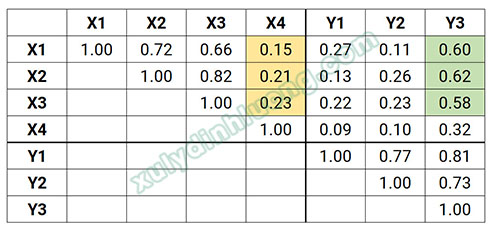
Để dễ hình dung hơn về tính phân biệt, chúng ta xét bảng tương quan tập chỉ báo/tập biến quan sát của hai cấu trúc biến tiềm ẩn X (4 biến quan sát) và Y (3 biến quan sát) dạng thang đo kết quả như bên dưới.
Để đảm bảo tính hội tụ, chúng ta kỳ vọng rằng hệ số tương quan giữa các chỉ báo được dùng để đo cùng một thang đo sẽ cao. Đầu tiên, quan sát hệ số tương quan giữa X1, X2, X3, X3 (đo lường cho X), hệ số tương quan các cặp X1-X2, X1-X3, X2-X3 khá cao (lần lượt là 0.72, 0.66, 0.82) trong khi hệ số tương quan của các cặp X1-X4, X2-X4, X3-X4 rất thấp (lần lượt là 0.15, 0.21 và 0.23). Như vậy, có thể tạm suy luận rằng dường như X4 không đo lường cho X. Nói chính xác hơn, X4 có thể không phải là một kết quả (hoặc là một kết quả rất yếu) từ X. Tiếp theo, quan sát hệ số tương quan giữa Y1, Y2, Y3, có thể thấy rằng hệ số tương quan giữa ba biến này khá cao (từ 0.70 trở lên), có thể tạm suy luận rằng ba chỉ báo này thực sự là kết quả (mạnh) của Y.
Để đảm bảo tính phân biệt giữa các tập chỉ báo, hai nhóm chỉ báo này cần có mức tương quan yếu với nhau. Hãy quan sát sự tương quan giữa X1, Y1, Y2, và Y3, chúng ta sẽ thấy ngay là X1 tương quan yếu với Y1 và Y2 nhưng tương quan ở mức trên trung bình với Y3. Tương tự như vậy với X2 và X3, X2 và X3 cũng tương quan ở mức trên trung bình với Y3. X4 có tương quan yếu với ba biến Y1, Y2, Y3. Một điều đáng lưu ý ở đây là Y3 tương quan trên trung bình với X1, X2 và X3, đồng thời Y3 cũng tương quan khá cao với Y1 và Y2. Như thế, dường như chỉ báo Y3 không đảm bảo tính phân biệt ở giữa X và Y (Y3 có thể đều là kết quả của cả X và Y).
** Bài viết này sử dụng trích dẫn và tham khảo nội dung từ Nguyễn Minh Hà & Vũ Hữu Thành, Giáo trình Phân tích dữ liệu: Áp dụng mô hình PLS - SEM, 2020, NXB Kinh tế TP. Hồ Chí Minh.